Breaking Down Bond Risks: Duration, DV01, and Convexity Explained
Newsletter #50
🕒 Macaulay Duration
Macaulay Duration measures the weighted average time it takes to receive all of a bond’s cash flows (both coupons and principal). In essence, it tells you how long, on average, your money is tied up in the bond before being paid back.
Where:
PV(CF_t) is the present value of the cash flow at time t
👉 Example: If a bond has a Macaulay Duration of 5 years and you purchase it for $90, it means that, on average, you’ll recoup your $90 investment through the bond’s cash flows over the next 5 years.
📈 Modified Duration
Modified Duration estimates how much a bond’s price will change, in percentage terms, for a 1% (or 100 basis point) change in yield.
Where:
y is the bond's yield to maturity
n is the number of compounding periods per year (usually it’s 2 for semi-annual compounding)
👉 Example: If a bond has a modified duration of 5, a 1% increase in yield would lead to an approximate 5% drop in the bond’s price.
🔄 DV01
In practice, traders often rely on DV01 (Dollar Value of 1 basis point ) to measure interest rate risk.
DV01 tells you how much the price of a bond changes in actual dollar terms when the yield moves by 1 basis point (0.01%).
It’s more practical than modified duration because it expresses risk in dollar terms — the same units traders use to track P&L — rather than as a percentage change.
👉 Example: If a bond has a DV01 of $10k, a 1bp (0.01%) move in the bond yield will result in a ~$10k move in their bond position.
📈 Convexity
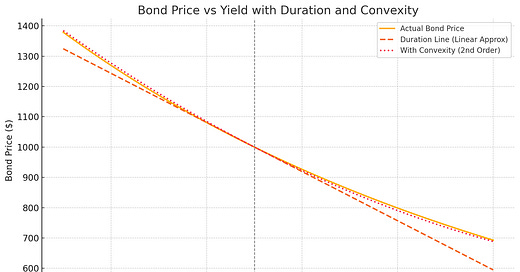
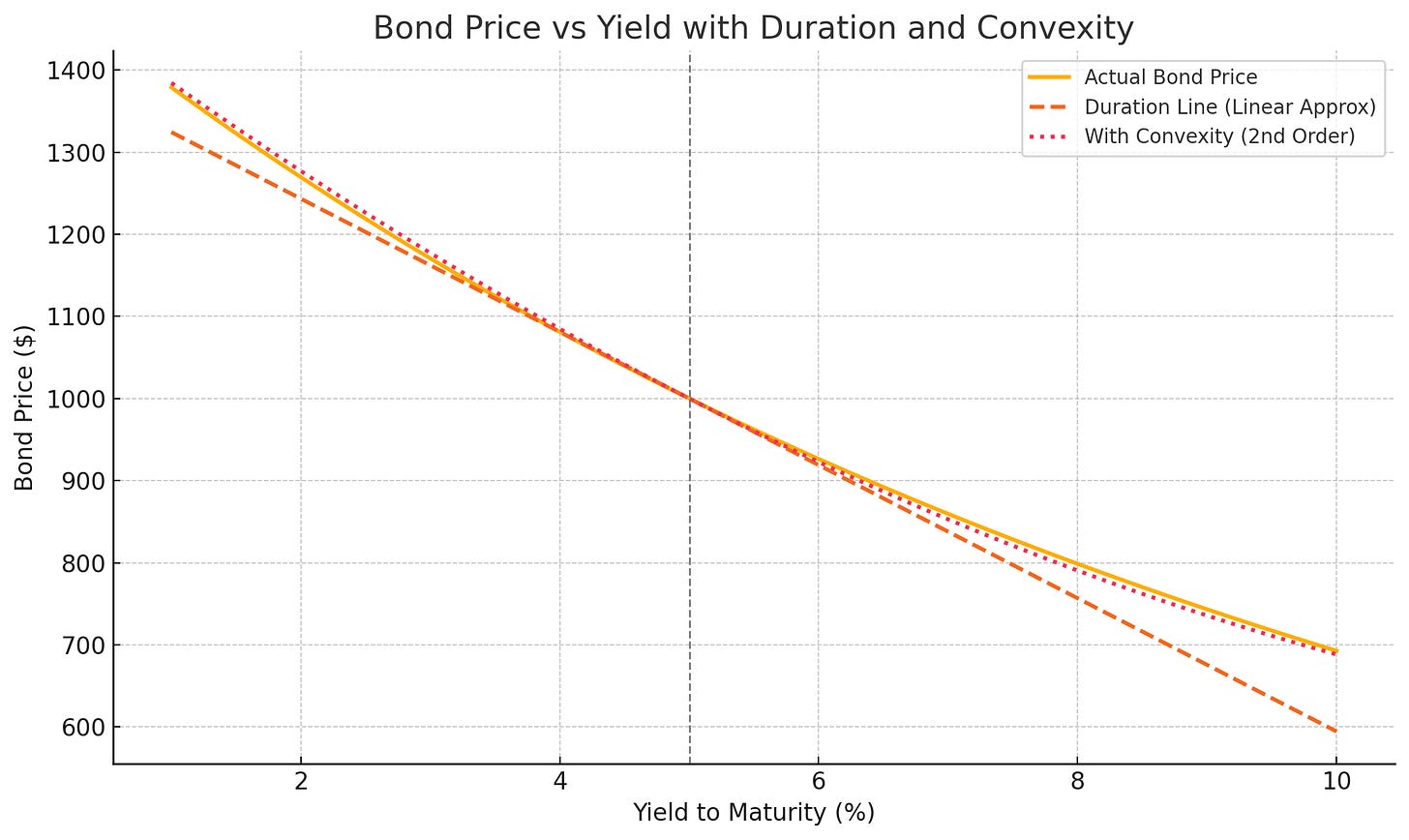
Convexity measures how a bond’s duration changes as yields change. In other words, it captures the curvature in the bond price–yield relationship.
Duration gives you a first-order approximation of price change; convexity gives you the second-order correction. Using the Taylor expansion we get:
Bonds with high convexity offer a valuable advantage. It enhances a bond’s performance by making gains larger when yields fall, and losses smaller when yields rise (due to the upward curvature in the price-yield relationship).
If two bonds have the same duration, the one with higher convexity will gain more when interest rates drop and lose less when they rise.
In this way, higher convexity provides both downside protection and upside potential.
Interview Guide (OUT NOW)
What’s inside the Quant Prep Interview Guide:
Time-Saving Strategies: Proven tips to land interviews efficiently, skipping the grind of endless applications.
Interview Mastery: A step-by-step breakdown of the process, packed with best practices and winning strategies.
Salary Insights: A detailed list of front-office compensation figures.
Industry Directory: A comprehensive roundup of top financial services firms.
Real-World Prep: 6 authentic interview experiences, covering 18 rounds of questions.
Extensive Question Bank: 138 carefully curated questions spanning Finance, Probability & Statistics, Math & Linear Algebra, Python, Algorithms, and HR.
HR Excellence: Tested techniques to shine in HR interviews.
Now on Sale: Just $21.60 (VAT included) - a steep discount from the regular $39.60.
Ready to land a $200k+ quant role? Grab your copy HERE.
Other Media
Twitter: @quant_prep
Medium: @quant_prep
LinkedIn: Quant Prep
Free Stoikov Market Making Code: Here
Free BTC Options Notebook: Here
Free CV template: Here